Using Meshmagick

Note

  • Mesh files examples used through this page are available under the meshmagick/tests/data directory so that you can play with them.

  • Images that illustrate the examples have been obtained with the Meshmagick’s viewer and by pressing the c keystroke.

  • Most of the command line options may be combined.

Content

Getting help

You can get command line help by issuing the following command:

>$ meshmagick -h

The output of this command is reproduced in the Command Line Interface Reference Guide.

Converting a mesh file

Converting a mesh file is one of the most basic usage of Meshmagick:

>$ meshmagick SEAREV.vtp -o SEAREV.mar

The format of the file is generally guessed from the extensions. Sometimes the extension may not be explicit enough to guess the file format. You should then use the -ifmt (--input-format) and -ofmt (--output-format) options to explicitly declare the file format:

>$ meshmagick SEAREV.vtp -ifmt paraview SEAREV.vtp -ofmt nemoh SEAREV.dat

This way, we told Meshmagick that SEAREV.dat must be in the Nemoh input mesh file format.

Quiet mode

To switch off outputs of Meshmagick, use the -q (--quiet) option:

>$ meshmagick SEAREV.vtp -q

Getting information on a mesh

Quick information

Quick information on a mesh is given by the -i (--info) option:

>$ meshmagick SEAREV.vtp -i

That gives us the following output:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

        --------------------------------------------
        	MESH NAME : SEAREV
        --------------------------------------------

        Number of vertices: 14354
        Number of faces:    15804

        Number of triangles:   2904
        Number of quadrangles: 12900

        xmin = -4.999371	xmax = 4.998167
        ymin = -15.000000	ymax = 15.000000
        zmin = -5.000000	zmax = 6.000000


        

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Mesh quality metrics

You can get some quality metrics on the mesh by issuing:

>$ meshmagick SEAREV.vtp --quality

that gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

Triangle quality of the mesh (2904 elements):

 Area Ratio:
    range: 0.0315238  -  0.104016
    average: 0.060761  , standard deviation: 0.0129906
 Edge Ratio:
    range: 1.0115  -  1.68482
    average: 1.28402  , standard deviation: 0.135239
 Aspect Ratio:
    range: 1.00504  -  1.78696
    average: 1.17559  , standard deviation: 0.104713
 Radius Ratio:
    range: 1.0001  -  1.63074
    average: 1.06858  , standard deviation: 0.0637777
 Frobenius Norm:
    range: 1.00009  -  1.4086
    average: 1.0574  , standard deviation: 0.0487658
 Minimal Angle:
    range: 35.6524  -  59.4647
    average: 48.5477  , standard deviation: 4.93326

Quadrilateral quality of the mesh (12900 elements):

 Area Ratio:
    range: 0.0774506  -  0.0812261
    average: 0.0797408  , standard deviation: 0.00129459
 Edge Ratio:
    range: 1.93626  -  2.03065
    average: 1.99352  , standard deviation: 0.0323648
 Aspect Ratio:
    range: 1.46813  -  1.51532
    average: 1.49676  , standard deviation: 0.0161824
 Radius Ratio:
    range: 1.22636  -  1.26155
    average: 1.24764  , standard deviation: 0.0120902
 Average Frobenius Norm:
    range: 1.22636  -  1.26155
    average: 1.24764  , standard deviation: 0.0120902
 Maximal Frobenius Norm:
    range: 1.22636  -  1.26155
    average: 1.24764  , standard deviation: 0.0120902
 Minimal Angle:
    range: 90  -  90
    average: 90  , standard deviation: 0


Definition of the different quality measures is given
        in the verdict library manual :
        http://www.vtk.org/Wiki/images/6/6b/VerdictManual-revA.pdf


=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Note

This option requires that you have installed a version of the python VTK library as it is used to compute these metrics. It relies on the verdict library, initially developed at Sandia lab and later included into VTK. More information on the metrics can be seen in the Verdict manual.

Mesh file visualization

Quickly viewing a mesh can be achieved by using the following command:

>$ meshmagick SEAREV.vtp --show

that opens the internal Meshmagick’s viewer.

../_images/viewer.png

Note

The viewer relies on VTK, so the python VTK library must be installed in order to use it.

The viewer is blazing fast and support mesh manipulation with the mouse. Some keyboard keys are available and their usage is indicated in the upper right panel.

Certainly the most useful feature is the visualization of normals by pressing the n keystroke so that you can verify consistency of normals across the mesh as well as orientation (must generally be outward for computations).

../_images/viewer_options.png

The above screenshot has been obtained by pressing successively the keys n (showing normals), w (wire representation), h (show Oxy plane i.e. the water free surface) and c (to save a screenshot that is saved under the name screenshot.png in the current working directory.)

Just play with options to discover what is available !

Note

The frame at the lower left corner is draggable and resizable so that you can inspect your mesh for alignment or whatever you want.

Mesh file concatenation

It is possible to concatenate two mesh files and write it into a global file by simply using this command:

>$ meshmagick myMesh.ext1 -cc mySecondMesh.ext1 -o outMesh.ext2

If the two files define faces that are joining, common vertices will me merged. This is of practical interest in BEM when dealing with multibody interactions of when lid are added to a mesh to remove irregular frequencies.

Note

File format for the two files to be concatenated has to be the same. The -ifmt command is used for both the files. The file format for the output file is driven normally (extension or -ofmt command).

Mesh healing

Meshmagick offers some options to deal with mesh description. Sometimes, meshes are produced with duplicated vertices description, making it impossible to establish some advanced connectivities. This is intrinsically the case for e.g. in GDF files, the input mesh file format of Wamit where faces are internally represented by vertices coordinates only, without using a connectivity table.

Sometimes also, faces normals are not consistent. This is often the case by e.g. when using GMSH mesh generator. You may also want to flip every normals.

Removing duplicate vertices

The -md (--merge-duplicates) option does this:

>$ meshmagick coque.gdf -md

that gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/coque.gdf successfully loaded
* Merging duplicate vertices that lie in an absolute proximity of 1.0E-08...
	--> Initial number of vertices : 15100
	--> Final number of vertices   : 3911
	--> 11189 vertices have been merged


=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

This allows to generate connectivity tables in the mesh and may drastically reduce the mesh size in memory and on disk.

Healing normals

This is obtained by using the -hn (--heal-normals) command line option. Let’s have an example. In the meshmagick/tests/data folder, you can find the file cylinder.geo that is a geometry file using the GMSH language for modeling geometry. It models the eighth of a cylinder.

If you have GMSH on your computer, you can generate a mesh file from this file by issuing the following command in your terminal:

>$ gmsh -2 cylinder.geo

It will generate a file named cylinder.msh which is a surface mesh of the portion of cylinder. One thing that you can do is to visualize this mesh with the --show option:

>$ meshmagick cylinder.msh --show

and stroke n to watch normals.

../_images/cylinder_msh_normals.png

It is clear that GMSH did not orient the normals consistently. Now, you can heal them by issuing by e.g.:

>$ meshmagick cylinder.msh -hn -o cylinder_healed.vtp --show

which heals the normals, opens the Meshmagick’s viewer and writes the healed mesh as a vtp file that can be opened into Paraview.

../_images/cylinder_msh_normals_healed.png

Note

This option uses a flood fill algorithm to diffuse the normal orientation information. For doing so, it requires to establish a connectivity map for faces/faces adjacency. For this map to be realized, it is necessary to merge duplicate nodes before healing normals. When invoking the -md (--merge-duplicates) and -hn (--heal-normals) options at the same time, merging is done before healing so it is verified.

Warning

If your mesh is not conformal, this option may fail as the connectivity map used by the flooding algorithm may present some non connected patches of faces that will be flooded independently, making the transit of normal orientation between these patch impossible.

Note

If the mesh is closed and conformal, a side effect of this option is to test if the normals are outgoing and correct them if they are not. This is achieved by “plunging the mesh in water” and integrate the hydrostatics pressure to identify the resultant force orientation which must be along the positive vertical in case the normals are outgoing. If the mesh does not allow this checking, normals are nevertheless made consistent and you are warned about the eventual need to manually watch the normals from the Meshmagick’s viewer and issue a new command to flip the whole normals as described in the following.

Flipping normals

This can be done with the -fn (--flip-normals) option. Based on the cylinder.vtp file obtained just before, if we issue the following command:

>$ meshmagick cylinder.vtp -fn --show

we get:

../_images/cylinder_msh_normals_flipped.png

Global healing

When getting a mesh file from somewhere, you could use the -hm (--heal-mesh) option to automatically apply a set of sanity checks and modifications on the mesh. It successively applies the following operations:

  • Removes unused vertices

  • Removes degenerated faces

  • Merge duplicate vertices

  • Heal triangles description

  • Heal normal orientations

The command is then:

>$ meshmagick cylinder.msh -hm

that outputs:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/cylinder.msh successfully loaded

OPERATION: heal the mesh
* Removing unused vertices in the mesh:
	--> 1 unused vertices have been removed
* Removing degenerated faces
	--> No degenerated faces
* Merging duplicate vertices that lie in an absolute proximity of 1.0E-08...
	--> No duplicate vertices have been found
* Ensuring consistent definition of triangles:
	--> Triangle description is consistent
FOUND OPEN BOUNDARY!!!
* Healing normals to make them consistent and if possible outward
	--> 2000 faces have been reversed to make normals consistent across the mesh
	--> WARNING: the mesh does not seem watertight althought marked as closed...
	Done.

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Mesh transformations

Some basic mesh transformation options are available: translations, rotations, scaling.

Translations

The options to use are -tx (--translatex), -ty (--translatey), -tz (--translatez), -t (--translate) which respectively performs translations along the x axis, the y axis, the z axis and along a coordinate vector. The invocations are:

>$ meshmagick SEAREV.vtp -tx 10
>$ meshmagick SEAREV.vtp -ty 10
>$ meshmagick SEAREV.vtp -tz 10

>$ meshmagick SEAREV.vtp -t 10 10 10 -i

for translations of 10 along specific axes and along the coordinate vector (10, 10, 10). The last command gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

OPERATION: Translation by [10.000000, 10.000000, 10.000000]
	-> Done.

        --------------------------------------------
        	MESH NAME : SEAREV
        --------------------------------------------

        Number of vertices: 14354
        Number of faces:    15804

        Number of triangles:   2904
        Number of quadrangles: 12900

        xmin = 5.000629	xmax = 14.998167
        ymin = -5.000000	ymax = 25.000000
        zmin = 5.000000	zmax = 16.000000


        

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Rotations

The options to use are -rx (--rotatex), -ry (--rotatey), -rz (--rotatez), -r (--rotate) which respectively performs rotations around the x axis, the y axis, the z axis and a 3D rotation along fixed axis rotation vector. The invocations are:

>$ meshmagick SEAREV.vtp -rx 90
>$ meshmagick SEAREV.vtp -ry 90
>$ meshmagick SEAREV.vtp -rz 90

>$ meshmagick SEAREV.vtp -r 90 90 90 -i

for rotations of 90° around specific axes and around the rotation coordinate vector (90, 90, 90). The last command gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

OPERATION: Rotation by [90.000000, 90.000000, 90.000000] (degrees)
	-> Done.

        --------------------------------------------
        	MESH NAME : SEAREV
        --------------------------------------------

        Number of vertices: 14354
        Number of faces:    15804

        Number of triangles:   2904
        Number of quadrangles: 12900

        xmin = -5.000000	xmax = 6.000000
        ymin = -15.000000	ymax = 15.000000
        zmin = -4.998167	zmax = 4.999371


        

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Warning

  • When using the -r (--rotate) option, please keep in mind that the angles given are not the Cardan angles (Roll, Pitch, Yaw) but angles around a fixed rotation axis.

  • Angles must be given in degrees.

Scaling

The options to use are -sx (--scalex), -sy (--scaley), -sz (--scalez), -s (--scale) which respectively performs scaling along the x axis, the y axis, the z axis and a 3D scaling of the mesh. The invocations are:

>$ meshmagick SEAREV.vtp -sx 2
>$ meshmagick SEAREV.vtp -sy 2
>$ meshmagick SEAREV.vtp -sz 2

>$ meshmagick SEAREV.vtp -s 2 -i

for scaling of 2 along specific axes and of the whole mesh in space. The last command gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

OPERATION: Scaling by 2.000000
	-> Done.

        --------------------------------------------
        	MESH NAME : SEAREV
        --------------------------------------------

        Number of vertices: 14354
        Number of faces:    15804

        Number of triangles:   2904
        Number of quadrangles: 12900

        xmin = -9.998741	xmax = 9.996333
        ymin = -30.000000	ymax = 30.000000
        zmin = -10.000000	zmax = 12.000000


        

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Warning

Scaling is performed before any translations when both options are used. So the translation magnitudes must be adapted to be consistent with the new scale of the mesh.

Triangulating quadrangles

The -tq (--triangulate-quadrangles) allows to split every quadrangle faces in the mesh into two triangle:

>$ meshmagick cylinder.msh -tq --show

that displays the following:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/cylinder.msh successfully loaded

Triangulating quadrangles
	-->3000 quadrangles have been split in triangles

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================
../_images/triangulate.png

Warning

The splitting procedure is basic and keep in mind that no check is done on the quality of the generated triangles. If your mesh faces does not have a good aspect ratio, it could produce some really tiny triangles.

Working with planes

Planes may be used in different situation as seen below. They can be defined so as to perform mesh clipping (useful to provide the submerged part of the mesh to hydrodynamics BEM software such as Nemoh), symmetrizing (when only a part of the mesh has been generated as in the cylinder.geo gmsh geometry file example) or mirroring.

A plane is defined by its normal \(\vec{n}\) and a scalar parameter \(c\) following the equation \(\vec{n}.\vec{x} = c\), where \(\vec{x}\) is the coordinate vector of a point belonging to the plane.

The scalar parameter \(c\) is practically the orthogonal distance between the origin of the reference frame and the plane.

Working with planes is quite flexible as you have 3 mean to use them along with plane dependent options:

  • Defining the plane by 4 scalars: \(n_x, n_y, n_z, c\)

  • Using predefined plane keywords:

    • Oxy

    • Oxz

    • Oyz

    • /Oxy

    • /Oxz

    • /Oyz

  • Using the index of a plane that has been defined with the -p (--plane) option.

Defining planes

A plane may be defined at the command line level along with de -p (--plane) option:

>$ meshmagick SEAREV.vtp -p 0 0 1 0

defines the plane with normal (0, 0, 1) and the scalar parameter 0.

It is also possible to define the same plane by a predefined keyword argument:

>$ meshmagick SEAREV.vtp -p Oxy

Predefined keywords arguments are Oxy, Oxz, Oyz, /Oxy, /Oxz, /Oyz and are self descriptive. The slash indicates that the normals is reversed.

It is possible to define several planes at once such as in:

>$ meshmagick SEAREV.vtp -p Oxy -p /Oxz

When defining planes with the -p (--plane) option, the planes definitions are internally stored in a list in the order that you used in the command line and it is then possible to refer to them in other options by their index in the list, starting by 0. So in the above command line, the plane Oxy can be refereed as the plane index 0 and the /Oxz plane as the plane index 1.

Clipping a mesh by a plane

To clip a mesh against a plane, use the -c (--clip) option like in:

>$ meshmagick SEAREV.vtp -c 1 1 1 2 --show

that displays the following view:

../_images/clip.png

As said before, the above command is strictly equivalent to:

>$ meshmagick SEAREV.vtp -p 1 1 1 2 -c 0 --show

It is also possible to use several -c (--clip) option at a time:

>$ meshmagick SEAREV.vtp -c Oxy -c Oyz --show

that gives:

../_images/clip2.png

Note

It is possible to invoke the -c (--clip) option without any argument. In that case, a default Oxy plane is taken.

Note

The part of the mesh that is kept is that opposite to the plane’s normal orientation.

Symmetrizing a mesh about a plane

To symmetrize a mesh about a plane, use the --sym (--symmetrize) option. Taking back the cylinder.msh example generated sooner, we can issue:

>$ meshmagick cylinder.msh --sym Oxy --show

that gives:

../_images/cylinder_sym.png

Combining the options allow us to close the cylinder:

>$ meshmagick cylinder.msh --sym Oxy --sym Oxz --sym Oyz --show

that gives:

../_images/cylinder_sym3.png

Checking normals gives as expected:

../_images/cylinder_sym3_normals.png

that we can heal:

>$ meshmagick cylinder.msh --sym Oxy --sym Oxz --sym Oyz -hn --show
../_images/cylinder_sym3_normals_healed.png

and clip back:

>$ meshmagick cylinder.msh --sym Oxy --sym Oxz --sym Oyz -hn -c Oxy -c Oyz -c Oxz --show

making us confident with respect to the normal consistency and orientation (outward) of our open part of cylinder mesh:

../_images/cylinder_sym3_normals_healed_clip.png

Note

Faces quality on the vicinity of the clipping plane is not checked. You can then generate faces with very poor aspect ratio. This will be fixed in a future Meshmagick’s release by applying a projection procedure that is nontrivial to develop as it must not modify the geometry locally.

Getting inertial properties of the mesh

Meshmagick allows to calculate inertial properties of meshes based on some assumptions on the mass distribution:

  • A mesh which is uniformly filled with an homogeneous medium with a given density (the practical interest if for e.g. for ballast modeling).

  • A mesh considered as a shell having a constant thickness and made in a medium of a given density (approximation for floating structures).

Todo

Add keywords for available medium…

Warning

  • Inertial properties are:

    • The mass \(m\) (tons)

    • The position of the center of gravity in the mesh’s reference frame \(\vec{OG}\)

    • The (3x3) symmetric 3D rotational inertia matrix \(\mathbf{I}_O\)

  • The inertia matrix must be expressed with respect to a reduction point. Internally, inertia calculations are done in the mesh’s reference frame (where vertices coordinates are expressed) so the default inertia matrix is expressed at the mesh’s origin. Please see the --reduction-point and --at-cog options to specify an other reduction point.

  • Note also that the default unit for mass in Meshmagick is the ton ! This is of practical use in offshore applications.

Note

  • Pay attention that the inertia products Ixy, Ixz and Iyz have the real significance and they should be used with a minus sign when put in a 3D rotational inertia matrix as in \(\mathbf{I}_O = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xy} & -I_{yz} & I_{zz} \end{bmatrix}\).

  • Coefficients are given by:

    • \(I_{xx} = \iint_{S_w}(y^2+z^2)dS\)

    • \(I_{xy} = \iint_{S_w}xydS\)

    • \(I_{xz} = \iint_{S_w}xzdS\)

    • \(I_{yy} = \iint_{S_w}(x^2+z^2)dS\)

    • \(I_{yz} = \iint_{S_w}yzdS\)

    • \(I_{zz} = \iint_{S_w}(x^2+y^2)dS\)

Defining the medium density

The medium density, for both assumptions on mass distribution in the mesh, is done by using the --rho-medium option:

>$ meshmagick SEAREV.vtp --rho-medium 1023

Note

Density must be given in kg/m**3 unit.

Note

In the above command line, we specified a meshfile as an option although we have no mesh processing at all, the aim being to get the list of available medium. This is a limitation of the argparse Python module that is used in Meshmagick to parse command line options and arguments. This module does not allow to define optional arguments that overhelms the mandatoriness of the positional arguments. Except for the --help command line option, you always have to specify a mesh file while calling Meshmagick.

It is also possible to use some default medium density keywords. These keywords can be retrieved using the --list-medium option:

>$ meshmagick SEAREV.vtp --list-medium

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

+----------------------+----------------------+
|NAME                  |     DENSITY (KG/M**3)|
+----------------------+----------------------+
|CONCRETE              |              2300.000|
+----------------------+----------------------+
|REINFORCED_CONCRETE   |              2400.000|
+----------------------+----------------------+
|FRESH_WATER           |              1000.000|
+----------------------+----------------------+
|SALT_WATER            |              1025.000|
+----------------------+----------------------+
|SAND                  |              1600.000|
+----------------------+----------------------+
|STEEL                 |              7850.000|
+----------------------+----------------------+
|ALUMINUM              |              2700.000|
+----------------------+----------------------+
|LEAD                  |             11350.000|
+----------------------+----------------------+
|TITANIUM              |              4500.000|
+----------------------+----------------------+
|POLYSTYRENE           |              1050.000|
+----------------------+----------------------+
|GASOLINE              |               750.000|
+----------------------+----------------------+
|DIESEL_FUEL           |               850.000|
+----------------------+----------------------+
|ETHANOL               |               789.000|
+----------------------+----------------------+
|AIR_20DEGC            |                 1.204|
+----------------------+----------------------+
|BUTANE                |                 2.700|
+----------------------+----------------------+
|PROPANE               |                 2.010|
+----------------------+----------------------+
|HYDROGEN_-252DEGC     |                70.000|
+----------------------+----------------------+
|NITROGEN_-195DEGC     |               810.000|
+----------------------+----------------------+


=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

An other solution is to look at the --help output.

Todo

  • Faire que argparse émette un warning si on a des options non reconnues.

  • Ajouter la possibilité d’exprimer les matrices résultat en un point de réduction particulier. Cette option qu’on nomera –reduction-point (-rp) sera utilisee a la fois par les inerties et par la matrice raideur

  • On mettra aussi en place une option –at-cog pour que le poitn de reduction soit specifie au cetre de gravite

Guessing the mesh is filled with homogeneous medium

This is achieved by using the -pi (--plain-inertia) option:

>$ meshmagick SEAREV.vtp -pi --rho-medium 800

that gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

Inertial parameters for a uniform distribution of a medium of density 800.0 kg/m**3 in the mesh:

	Mass = 2117.400 tons
	COG (m):
		xg = -0.207
		yg = -0.000
		zg = 0.547
	Inertia matrix (SI):
		1.764E+08	-1.455E-09	1.986E+06
		-1.455E-09	3.110E+07	-0.000E+00
		1.986E+06	-0.000E+00	1.723E+08
	Expressed at point : 		0.000E+00	0.000E+00	0.000E+00

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Note

If the medium’s density is not specified, the -pi option guesses that the medium is salt water and then takes a default density of 1023 kg/m**3.

Guessing the mesh is a shell

This is achieved by using the -si (--shell-inertia) option:

>$ meshmagick SEAREV.vtp -si --rho-medium 5850 --thickness 0.02

that gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded

Inertial parameters for a shell distribution of a medium of density 5850.0 kg/m**3 and a thickness of 0.020 m over the mesh:

	Mass = 140.997 tons
	COG (m):
		xg = -0.266
		yg = 0.000
		zg = 0.647
	Inertia matrix (SI):
		1.578E+07	-1.375E+01	2.205E+05
		-1.375E+01	3.799E+06	-6.452E+00
		2.205E+05	-6.452E+00	1.536E+07
	Expressed at point : 		0.000E+00	0.000E+00	0.000E+00

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

Note

  • If the --rho-medium option is not specified, the medium density is by default considered that of steel (5850 kg/m**3)

  • If the --thickness option is not specified, the thickness of the shell is by default considered being 0.02 meters.

Performing hydrostatics calculations on the mesh

Meshmagick allows to perform some hydrostatics computations on meshes. You can get the current hydrostatics properties of the mesh such as the hydrostatic stiffness matrix, metacentric heights, floating plane area…

It is also able to compute the hydrostatic equilibrium of the mesh with respect to a given floater mass and/or a given position of the center of gravity as well as additional external forces.

Expression of the hydrostatic data

The hydrostatic stiffness matrix coefficients only depend on the geometry of the flotation plane that is the polygon (s) generated by the intersection of the body with the horizontal plane Oxy. The matrix writes:

\[\begin{split}K_{hs} = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & K_{33} & K_{34} & K_{35} & 0 \\ 0 & 0 & K_{43} & K_{44} & K_{45} & 0 \\ 0 & 0 & K_{53} & K_{54} & K_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}\end{split}\]

This matrix is symmetric so that we have \(K_{43}=K_{34}\), \(K_{53}=K_{35}\) and \(K_{54}=K_{45}\) and we will only present 6 coefficients in the hydrostatic reports.

The expression of the hydrostatic coefficients is:

\begin{eqnarray} K_{33} &=& \rho g S_f\\ K_{34} &=& \rho g \iint_{S_f} y dS\\ K_{35} &=& -\rho g \iint_{S_f} x dS\\ K_{45} &=& -\rho g \iint_{S_f} xy dS\\ R_t &=& \frac{1}{\nabla} \iint_{S_f} y^2 dS\\ R_l &=& \frac{1}{\nabla} \iint_{S_f} x^2 dS\\ a &=& z_g - z_b \\ GM_t &=& R_t - a\\ GM_l &=& R_l - a\\ K_{44} &=& \rho g \nabla GM_t\\ K_{55} &=& \rho g \nabla GM_l\\ x_f &=& -\frac{K_{35}}{K_{33}}\\ x_f &=& \frac{K_{34}}{K_{33}} \end{eqnarray}

where \(\nabla\) is the volume displacement of the body, \(R_t\) and \(R_l\) are respectively the transversal and longitudinal metacentric radius, \(GM_t\) and \(GM_l\) are respectively the transversal and longitudinal metacentric heights, \(x_f\) and \(y_f\) are the horizontal position of the center of the flotation plane.

Getting hydrostatics properties of the mesh

To get an hydrostatic report on the current configuration of the mesh, you may use the -hs option along with the –zcog option to specify the z position of the center of gravity (mandatory):

>$ meshmagick SEAREV.vtp -hs --zcog -2

that gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded
>>>> Performing hydrostatic computation on the current hull configuration considered at equilibrium



HYDROSTATIC REPORT (Meshmagick version 3.2)

[1]	Corrections made on initial mesh:
	Z CORRECTION (M)----------------------------->   0.000
	HEEL CORRECTION (DEG)------------------------>   0.000
	TRIM CORRECTION (DEG)------------------------>  -0.000

	GRAVITY ACCELERATION (M/S**2)---------------->   9.81
	DENSITY OF WATER (KG/M**3)------------------->   1025.0

	WATERPLANE AREA (M**2)----------------------->   299.8
	WATERPLANE CENTER (M)------------------------>  -0.001     0.000     0.000    
	WETTED SURFACE AREA (M**2)------------------->   549.6
	DISPLACEMENT VOLUME (M**3)------------------->   1176.831
	DISPLACEMENT MASS (TONS)--------------------->   1206.252
	BUOYANCY CENTER (M)-------------------------->  -0.000     0.000    -2.121    
	CENTER OF GRAVITY (M)------------------------>  -0.000     0.000    -2.000    

	DRAFT (M)------------------------------------>   5.000
	LENGTH OVERALL SUBMERGED (M)----------------->   10.00
	BREADTH OVERALL SUBMERGED (M)---------------->   30.00
	LENGTH AT WATERLINE LWL (M)------------------>   9.99
	FORWARD PERPENDICULAR FP (M)----------------->   5.00
	[2] LENGTH BETWEEN PERPENDICULARS LPP (M)---->   9.99

	TRANSVERSAL METACENTRIC RADIUS (M)----------->   19.107
	LONGITUDINAL METACENTRIC RADIUS (M)---------->   2.120
	TRANSVERSAL METACENTRIC HEIGHT GMT (M)------->   18.986
	LONGITUDINAL METACENTRIC HEIGHT GML (M)------>   1.999

	HYDROSTATIC STIFFNESS COEFFICIENTS (at COG horiz. Pos.):
	K33 (N/M)------------------------------------>   3.0147E+06
	K34 (N)-------------------------------------->   0.0000E+00
	K35 (N)-------------------------------------->   1.5564E+03
	K44 (N.M)------------------------------------>   2.2467E+08
	K45 (N.M)------------------------------------>   0.0000E+00
	K55 (N.M)------------------------------------>   2.3661E+07

[2]	INERTIAS from standard approximations: [Rxx = 0.3 B; Ryy = Rzz = 0.25 Lpp]
	RXX (M)-------------------------------------->   9.000
	RYY (M)-------------------------------------->   2.498
	RZZ (M)-------------------------------------->   2.498
	IXX------------------------------------------>   9.771E+07
	IYY------------------------------------------>   7.530E+06
	IZZ------------------------------------------>   7.530E+06

	INERTIAS from homogeneous immersed hull approximation:
	RXX------------------------------------------>   9.233
	RYY------------------------------------------>   4.060
	RZZ------------------------------------------>   9.014
	IXX------------------------------------------>   1.028E+08
	IYY------------------------------------------>   1.989E+07
	IZZ------------------------------------------>   9.800E+07


NOTES
=====
[1] To get computed hydrostatic equilibrium position from initial mesh, corrections must be 
    applied in the following order:
    	* First rotations around initial X & Y axes w.r.t initial frame origin
    	* Second Z translation along initial Z-axis (not the one obtained after the rotations)
[2] Not enough information to get a trusted Lpp. It has been approximated by Lwl instead.
    It has an influence on the Iyy and Izz inertias calculated from standard approximations.
    To get more accurate results, please specify a Lpp.

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

In our case, taking a center of gravity so high results in an unstable configuration as you can see in the report, as the longitudinal metacentric height (GML) is negative.

Note

  • Among the results, you will find the inertia coefficients of the immersed part of the body. The assumptions done here are that the body is filled with water. Pay attention that the inertia products Ixy, Ixz and Iyz have the real significance and they should be used with a minus sign when put in a 3D rotational inertia matrix as in \(\mathbf{I}_O = \begin{bmatrix} I_{xx} & -I_{xy} & -I_{xz} \\ -I_{xy} & I_{yy} & -I_{yz} \\ -I_{xy} & -I_{yz} & I_{zz} \end{bmatrix}\).

  • Coefficients are given by:

    • \(I_{xx} = \iint_{S_w}(y^2+z^2)dS\)

    • \(I_{xy} = \iint_{S_w}xydS\)

    • \(I_{xz} = \iint_{S_w}xzdS\)

    • \(I_{yy} = \iint_{S_w}(x^2+z^2)dS\)

    • \(I_{yz} = \iint_{S_w}yzdS\)

    • \(I_{zz} = \iint_{S_w}(x^2+y^2)dS\)

Note

You can easily change the default density of water as well as gravity by using the --rho-water and --grav options.

Getting the mesh vertical position that complies with a given mass displacement

In that mode, the mesh is displaced so that its mas displacement becomes equal to a specified mass. This is achieved by:

>$ meshmagick SEAREV.vtp -hs --zcog -2 -mdisp 1500

which gives:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded
>>>> Computing equilibrium of the hull for the given displacement of 1500.000000 tons
========================
Displacement equilibrium
========================
Target displacement:    1500.000 tons
Achieved displacement: 1500.000 tons (3 iterations)



HYDROSTATIC REPORT (Meshmagick version 3.2)

[1]	Corrections made on initial mesh:
	Z CORRECTION (M)----------------------------->  -0.962
	HEEL CORRECTION (DEG)------------------------>   0.000
	TRIM CORRECTION (DEG)------------------------>  -0.000

	GRAVITY ACCELERATION (M/S**2)---------------->   9.81
	DENSITY OF WATER (KG/M**3)------------------->   1025.0

	WATERPLANE AREA (M**2)----------------------->   294.3
	WATERPLANE CENTER (M)------------------------>  -0.002    -0.000     0.962    
	WETTED SURFACE AREA (M**2)------------------->   626.7
	DISPLACEMENT VOLUME (M**3)------------------->   1463.414
	DISPLACEMENT MASS (TONS)--------------------->   1500.000
	BUOYANCY CENTER (M)-------------------------->  -0.000     0.000    -1.612    
	CENTER OF GRAVITY (M)------------------------>  -0.000     0.000    -2.000    

	DRAFT (M)------------------------------------>   5.962
	LENGTH OVERALL SUBMERGED (M)----------------->   10.00
	BREADTH OVERALL SUBMERGED (M)---------------->   30.00
	LENGTH AT WATERLINE LWL (M)------------------>   9.81
	FORWARD PERPENDICULAR FP (M)----------------->   4.90
	[2] LENGTH BETWEEN PERPENDICULARS LPP (M)---->   9.81

	TRANSVERSAL METACENTRIC RADIUS (M)----------->   15.084
	LONGITUDINAL METACENTRIC RADIUS (M)---------->   1.613
	TRANSVERSAL METACENTRIC HEIGHT GMT (M)------->   15.472
	LONGITUDINAL METACENTRIC HEIGHT GML (M)------>   2.001

	HYDROSTATIC STIFFNESS COEFFICIENTS (at COG horiz. Pos.):
	K33 (N/M)------------------------------------>   2.9595E+06
	K34 (N)-------------------------------------->   0.0000E+00
	K35 (N)-------------------------------------->   6.0626E+03
	K44 (N.M)------------------------------------>   2.2768E+08
	K45 (N.M)------------------------------------>   0.0000E+00
	K55 (N.M)------------------------------------>   2.9452E+07

[2]	INERTIAS from standard approximations: [Rxx = 0.3 B; Ryy = Rzz = 0.25 Lpp]
	RXX (M)-------------------------------------->   9.000
	RYY (M)-------------------------------------->   2.453
	RZZ (M)-------------------------------------->   2.453
	IXX------------------------------------------>   1.215E+08
	IYY------------------------------------------>   9.024E+06
	IZZ------------------------------------------>   9.024E+06

	INERTIAS from homogeneous immersed hull approximation:
	RXX------------------------------------------>   9.637
	RYY------------------------------------------>   4.951
	RZZ------------------------------------------>   9.035
	IXX------------------------------------------>   1.393E+08
	IYY------------------------------------------>   3.676E+07
	IZZ------------------------------------------>   1.224E+08


NOTES
=====
[1] To get computed hydrostatic equilibrium position from initial mesh, corrections must be 
    applied in the following order:
    	* First rotations around initial X & Y axes w.r.t initial frame origin
    	* Second Z translation along initial Z-axis (not the one obtained after the rotations)
[2] Not enough information to get a trusted Lpp. It has been approximated by Lwl instead.
    It has an influence on the Iyy and Izz inertias calculated from standard approximations.
    To get more accurate results, please specify a Lpp.

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

This mode is active as long as you don’t use the --cog option that trig the 3D equilibrium searching algorithm that is presented in the following.

Warning

The mass has to be given in tons as it is more representative of the order of magnitude of usual masses in offshore.

3D hydrostatic equilibrium

This mode is active as long as you use the --cog option such that:

>$ meshmagick SEAREV.vtp -hs --cog 0 4 -2

That command outputs the following report:

=============================================
meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
=============================================
../meshmagick/tests/data/SEAREV.vtp successfully loaded
>>>> Computing equilibrium in 3DOF for the given COG, considering the current configuration presents the target displacement
========================
3DOF equilibrium
========================
Target diplacement:    1206.252 tons
COG pos:  [0.0, 4.0, -2.0]
	>>> Convergence reached in 9 iterations



HYDROSTATIC REPORT (Meshmagick version 3.2)

[1]	Corrections made on initial mesh:
	Z CORRECTION (M)----------------------------->   0.005
	HEEL CORRECTION (DEG)------------------------>  -12.114
	TRIM CORRECTION (DEG)------------------------>   0.148

	GRAVITY ACCELERATION (M/S**2)---------------->   9.81
	DENSITY OF WATER (KG/M**3)------------------->   1025.0

	WATERPLANE AREA (M**2)----------------------->   286.3
	WATERPLANE CENTER (M)------------------------>  -0.037     0.107     0.018    
	WETTED SURFACE AREA (M**2)------------------->   549.0
	DISPLACEMENT VOLUME (M**3)------------------->   1176.831
	DISPLACEMENT MASS (TONS)--------------------->   1206.252
	BUOYANCY CENTER (M)-------------------------->  -0.001     3.937    -1.707    
	CENTER OF GRAVITY (M)------------------------>   0.000     4.000    -2.000    

	DRAFT (M)------------------------------------>   8.032
	LENGTH OVERALL SUBMERGED (M)----------------->   10.01
	BREADTH OVERALL SUBMERGED (M)---------------->   31.14
	LENGTH AT WATERLINE LWL (M)------------------>   10.00
	FORWARD PERPENDICULAR FP (M)----------------->   5.00
	[2] LENGTH BETWEEN PERPENDICULARS LPP (M)---->   10.00

	TRANSVERSAL METACENTRIC RADIUS (M)----------->   20.785
	LONGITUDINAL METACENTRIC RADIUS (M)---------->   1.788
	TRANSVERSAL METACENTRIC HEIGHT GMT (M)------->   21.084
	LONGITUDINAL METACENTRIC HEIGHT GML (M)------>   2.088

	HYDROSTATIC STIFFNESS COEFFICIENTS (at COG horiz. Pos.):
	K33 (N/M)------------------------------------>   2.8786E+06
	K34 (N)-------------------------------------->  -9.7380E+06
	K35 (N)-------------------------------------->   8.6414E+04
	K44 (N.M)------------------------------------>   2.4950E+08
	K45 (N.M)------------------------------------>   9.3365E+05
	K55 (N.M)------------------------------------>   2.4706E+07

[2]	INERTIAS from standard approximations: [Rxx = 0.3 B; Ryy = Rzz = 0.25 Lpp]
	RXX (M)-------------------------------------->   9.343
	RYY (M)-------------------------------------->   2.499
	RZZ (M)-------------------------------------->   2.499
	IXX------------------------------------------>   1.053E+08
	IYY------------------------------------------>   7.535E+06
	IZZ------------------------------------------>   7.535E+06

	INERTIAS from homogeneous immersed hull approximation:
	RXX------------------------------------------>   10.065
	RYY------------------------------------------>   4.826
	RZZ------------------------------------------>   9.515
	IXX------------------------------------------>   1.222E+08
	IYY------------------------------------------>   2.810E+07
	IZZ------------------------------------------>   1.092E+08


NOTES
=====
[1] To get computed hydrostatic equilibrium position from initial mesh, corrections must be 
    applied in the following order:
    	* First rotations around initial X & Y axes w.r.t initial frame origin
    	* Second Z translation along initial Z-axis (not the one obtained after the rotations)
[2] Not enough information to get a trusted Lpp. It has been approximated by Lwl instead.
    It has an influence on the Iyy and Izz inertias calculated from standard approximations.
    To get more accurate results, please specify a Lpp.

=============================================================
Meshmagick - version 3.2
Copyright 2014-2021, Ecole Centrale de Nantes / D-ICE Engineering
Maintainer : Francois Rongere <Francois.Rongere@dice-engineering.com>
Good Bye!
=============================================================

and displays the following viewer:

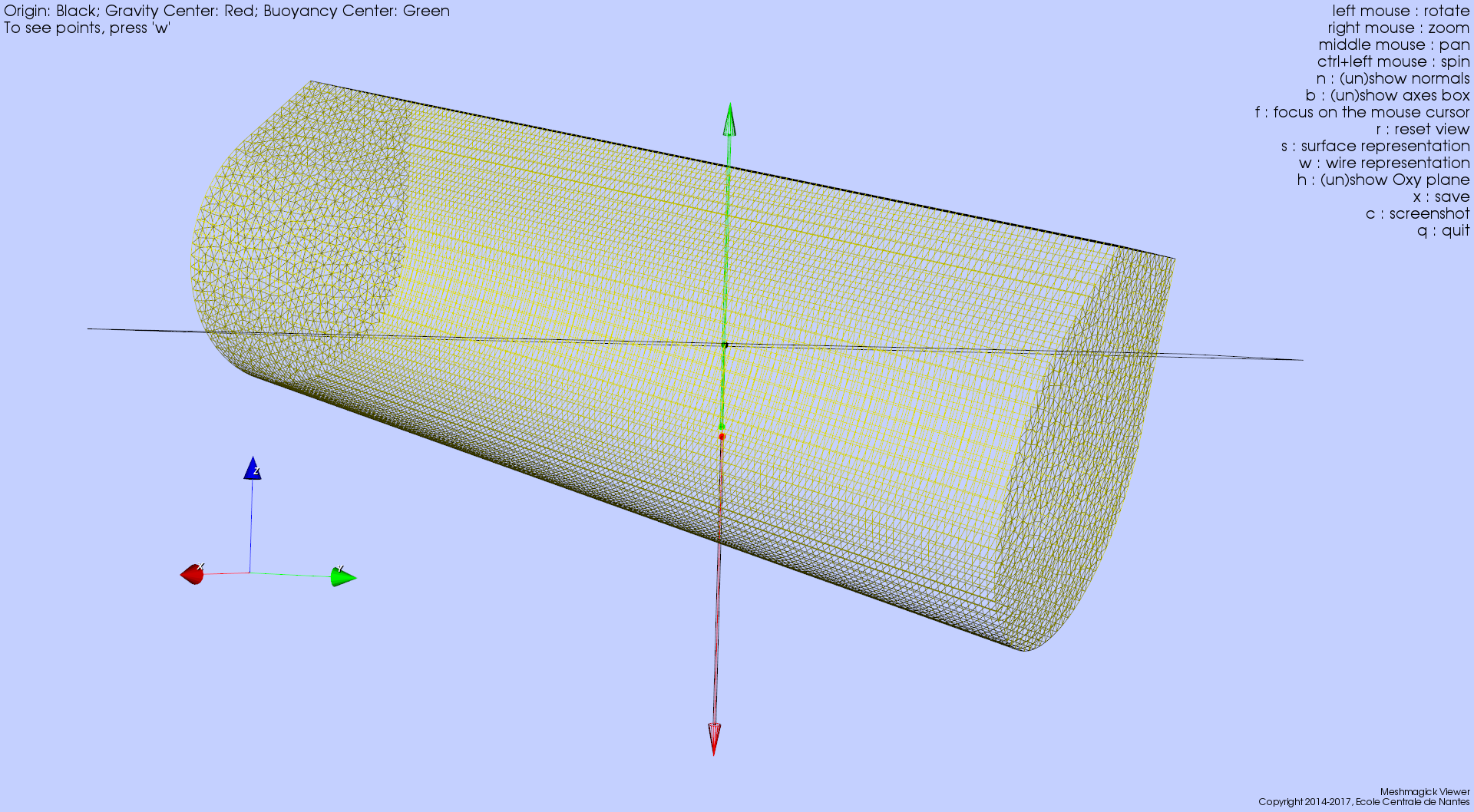
../_images/3D_hydrostatics.png

Note

The solver in charge of the hydrostatic equilibrium computation is iterative. It uses the hydrostatic stiffness matrix and the residual force to compute corrections in position and attitude of the floater (it solves a linear system at each iteration). Since we use here a linearized approximation that is only valid for tiny displacements and rotations, if the proposed correction is greater than some threshold, the correction is relaxed in magnitude. The solver is then a Newton type solver.

Sometimes, the solver could not converge to an equilibrium position (stable or not). This is detected by applying a maximum of iteration number. If that number is reached without any convergence then the floater is rotated with random angles to generate a new initial configuration for iterations (it is called here a restart). A maximum number of restart is allowed. This method makes the solver very robust with respect to the initial configuration given and it is possible to specify some position of the center of gravity that makes the floater capsize.

Warning

  • Pay attention that when 3D hydrostatic equilibrium is performed, rotations around x and y as well as translation along z are applied iteratively in order to minimize the residual force with respect to a relative tolerance based on mesh principal dimensions. During iterations, you may have a drift of the orientation of the mesh around the z axis. Although the hydrostatic stiffness coefficient are correctly computed, this unpredictable orientation result in an impractical stiffness matrix as it is then not expressed in a convenient axis system. This should be fixed in a later release of meshmagick. Please use the meshmagick viewer to see what is going on.

  • In order to perform 3D hydrostatic equilibrium searching possible, it is mandatory to use a watertight mesh so that the boundary intersection polygons are closed.

Saving the hydrostatic report in a text file

Use the --hs-report option followed by the name of the file:

>$ meshmagick SEAREV.vtp -hs --hs-report report.txt